github:
https://github.com/pandalabme/d2l/tree/main/exercises
import sys
import torch.nn as nn
import torch
import warnings
sys.path.append('/home/jovyan/work/d2l_solutions/notebooks/exercises/d2l_utils/')
import d2l
from torchsummary import summary
warnings.filterwarnings("ignore")
def nin_block(out_channels, kernel_size, strides, padding, conv1s=[[1,0],[1,0]]):
layers = [nn.LazyConv2d(out_channels, kernel_size=kernel_size, stride=strides, padding=padding),nn.ReLU()]
for conv1_size,conv1_padding in conv1s:
layers.append(nn.LazyConv2d(out_channels, kernel_size=conv1_size,padding=conv1_padding))
layers.append(nn.ReLU())
return nn.Sequential(*layers)
class Nin(d2l.Classifier):
def __init__(self, arch, lr=0.1):
super().__init__()
self.save_hyperparameters()
layers = []
for i in range(len(arch)-1):
layers.append(nin_block(*arch[i]))
layers.append(nn.MaxPool2d(3, stride=2))
layers.append(nn.Dropout(0.5))
layers.append(nin_block(*arch[-1]))
layers.append(nn.AdaptiveAvgPool2d((1, 1)))
layers.append(nn.Flatten())
self.net = nn.Sequential(*layers)
self.net.apply(d2l.init_cnn)
data = d2l.FashionMNIST(batch_size=128, resize=(224, 224))
arch = ((96,11,4,0),(256,5,1,2),(384,3,1,1),(10,3,1,1))
model = Nin(arch, lr=0.03)
model.apply_init([next(iter(data.get_dataloader(True)))[0]], d2l.init_cnn)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# Initialize memory counters
torch.cuda.reset_peak_memory_stats()
torch.cuda.empty_cache()
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
trainer.fit(model, data)
memory_stats = torch.cuda.memory_stats(device=device)
# Print peak memory usage and other memory statistics
print("Peak memory usage:", memory_stats["allocated_bytes.all.peak"] / (1024 ** 2), "MB")
print("Current memory usage:", memory_stats["allocated_bytes.all.current"] / (1024 ** 2), "MB")
X,y = next(iter(data.get_dataloader(False)))
X = X.to('cuda')
y = y.to('cuda')
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
torch.cuda.reset_peak_memory_stats()
torch.cuda.empty_cache()
y_hat = model(X)
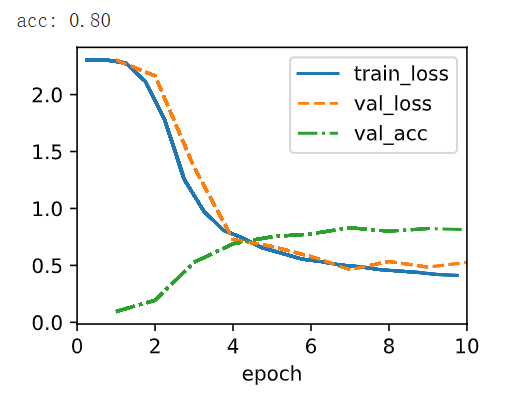
print(f'acc: {model.accuracy(y_hat,y).item():.2f}')
memory_stats = torch.cuda.memory_stats(device=device)
print("Peak memory usage:", memory_stats["allocated_bytes.all.peak"] / (1024 ** 2), "MB")
print("Current memory usage:", memory_stats["allocated_bytes.all.current"] / (1024 ** 2), "MB")
Nin(
(net): Sequential(
(0): Sequential(
(0): LazyConv2d(0, 96, kernel_size=(11, 11), stride=(4, 4))
(1): ReLU()
(2): LazyConv2d(0, 96, kernel_size=(1, 1), stride=(1, 1))
(3): ReLU()
(4): LazyConv2d(0, 96, kernel_size=(1, 1), stride=(1, 1))
(5): ReLU()
)
(1): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(2): Sequential(
(0): LazyConv2d(0, 256, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(1): ReLU()
(2): LazyConv2d(0, 256, kernel_size=(1, 1), stride=(1, 1))
(3): ReLU()
(4): LazyConv2d(0, 256, kernel_size=(1, 1), stride=(1, 1))
(5): ReLU()
)
(3): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(4): Sequential(
(0): LazyConv2d(0, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU()
(2): LazyConv2d(0, 384, kernel_size=(1, 1), stride=(1, 1))
(3): ReLU()
(4): LazyConv2d(0, 384, kernel_size=(1, 1), stride=(1, 1))
(5): ReLU()
)
(5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(6): Dropout(p=0.5, inplace=False)
(7): Sequential(
(0): LazyConv2d(0, 10, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU()
(2): LazyConv2d(0, 10, kernel_size=(1, 1), stride=(1, 1))
(3): ReLU()
(4): LazyConv2d(0, 10, kernel_size=(1, 1), stride=(1, 1))
(5): ReLU()
)
(8): AdaptiveAvgPool2d(output_size=(1, 1))
(9): Flatten(start_dim=1, end_dim=-1)
)
)
1. Why are there two 1\times1 convolutional layers per NiN block? Increase their number to three. Reduce their number to one. What changes?
In Network in Network (NiN) architecture, 1\times1 convolutional layers are used to introduce additional non-linearity and increase the capacity of the network without introducing too many parameters. The inclusion of these 1\times1 convolutions has specific effects on the network’s expressiveness and complexity:
-
Two 1\times1 Convolutional Layers per NiN Block:
- When there are two 1\times1 convolutional layers per NiN block, it creates multiple pathways for feature transformation. Each 1\times1 convolution performs its own set of operations, allowing the network to capture complex relationships between features and enable better representation learning.
- Having two 1\times1 convolutions can increase the model’s capacity and non-linearity, potentially leading to improved accuracy and more expressive features.
-
Three 1\times1 Convolutional Layers per NiN Block:
- Increasing the number of 1\times1 convolutional layers further amplifies the network’s capacity. Each additional convolutional layer introduces more non-linearity and the possibility of capturing more complex interactions between features.
- However, increasing the number of 1\times1 convolutions also increases the number of parameters and computations, potentially leading to overfitting and higher computational costs.
-
One 1\times1 Convolutional Layer per NiN Block:
- Using only one 1\times1 convolutional layer reduces the complexity of each NiN block. It limits the capacity of the network to capture complex feature interactions, and may lead to underfitting if the dataset and task are complex.
- Reducing the number of 1\times1 convolutions also decreases the number of parameters and computations, which can be beneficial for faster training and reduced memory usage.
Overall, the number of 1\times1 convolutional layers in NiN blocks impacts the network’s capacity, complexity, and computational requirements. The optimal choice depends on factors such as the dataset’s complexity, available computational resources, and desired trade-off between accuracy and efficiency. Experimentation and validation on a specific task are necessary to determine the most suitable configuration for the network.
arch = ((96,11,4,0,3),(256,5,1,2,3),(384,3,1,1,3),(10,3,1,1,3))
model = Nin(arch)
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
trainer.fit(model, data)
X,y = next(iter(data.get_dataloader(False)))
X = X.to('cuda')
y = y.to('cuda')
y_hat = model(X)
print(f'acc: {model.accuracy(y_hat,y).item():.2f}')
data = d2l.FashionMNIST(batch_size=128, resize=(224, 224))
arch = ((96,11,4,0,[[1,0]]),(256,5,1,2,[[1,0]]),(384,3,1,1,[[1,0]]),(10,3,1,1,[[1,0]]))
model = Nin(arch, lr=0.05)
model.apply_init([next(iter(data.get_dataloader(True)))[0]], d2l.init_cnn)
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
trainer.fit(model, data)
X,y = next(iter(data.get_dataloader(False)))
X = X.to('cuda')
y = y.to('cuda')
y_hat = model(X)
print(f'acc: {model.accuracy(y_hat,y).item():.2f}')
2. What changes if you replace the 1\times1 convolutions by 3\times3 convolutions?
arch = ((96,11,4,0,[[3,1],[3,1]]),(256,5,1,2,[[3,1],[3,1]]),(384,3,1,1,[[3,1],[3,1]]),(10,3,1,1,[[3,1],[3,1]]))
model = Nin(arch)
model.apply_init([next(iter(data.get_dataloader(True)))[0]], d2l.init_cnn)
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
trainer.fit(model, data)
X,y = next(iter(data.get_dataloader(False)))
X = X.to('cuda')
y = y.to('cuda')
y_hat = model(X)
print(f'acc: {model.accuracy(y_hat,y).item():.2f}')
3. What happens if you replace the global average pooling by a fully connected layer (speed, accuracy, number of parameters)?
class MLPNin(d2l.Classifier):
def __init__(self, arch, lr=0.1, num_classes=10):
super().__init__()
self.save_hyperparameters()
layers = []
for i in range(len(arch)-1):
layers.append(nin_block(*arch[i]))
layers.append(nn.MaxPool2d(3, stride=2))
layers.append(nn.Dropout(0.5))
layers.append(nin_block(*arch[-1]))
layers.append(nn.Flatten())
layers.append(nn.LazyLinear(num_classes))
self.net = nn.Sequential(*layers)
self.net.apply(d2l.init_cnn)
4. Calculate the resource usage for NiN.
4.1 What is the number of parameters?
arch = ((96,11,4,0,2),(256,5,1,2,2),(384,3,1,1,2),(10,3,1,1,2))
model = Nin(arch)
X = torch.randn(1,3, 224, 224)
_ = model(X)
total_params = sum(p.numel() for p in model.parameters())
print("Total parameters:", total_params)
Total parameters: 2015398
4.2 What is the amount of computation?
from thop import profile
flops, params = profile(model, inputs=(X,))
print("Total FLOPs:", flops)
[INFO] Register count_convNd() for <class 'torch.nn.modules.conv.Conv2d'>.
[INFO] Register zero_ops() for <class 'torch.nn.modules.activation.ReLU'>.
[INFO] Register zero_ops() for <class 'torch.nn.modules.container.Sequential'>.
[INFO] Register zero_ops() for <class 'torch.nn.modules.pooling.MaxPool2d'>.
[INFO] Register zero_ops() for <class 'torch.nn.modules.dropout.Dropout'>.
[INFO] Register count_adap_avgpool() for <class 'torch.nn.modules.pooling.AdaptiveAvgPool2d'>.
Total FLOPs: 830042124.0
4.3 What is the amount of memory needed during training?
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# Initialize memory counters
torch.cuda.reset_peak_memory_stats()
torch.cuda.empty_cache()
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
trainer.fit(model, data)
memory_stats = torch.cuda.memory_stats(device=device)
# Print peak memory usage and other memory statistics
print("Peak memory usage:", memory_stats["allocated_bytes.all.peak"] / (1024 ** 2), "MB")
print("Current memory usage:", memory_stats["allocated_bytes.all.current"] / (1024 ** 2), "MB")
4.4 What is the amount of memory needed during prediction?
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
torch.cuda.reset_peak_memory_stats()
torch.cuda.empty_cache()
_ = model(X)
memory_stats = torch.cuda.memory_stats(device=device)
print("Peak memory usage:", memory_stats["allocated_bytes.all.peak"] / (1024 ** 2), "MB")
print("Current memory usage:", memory_stats["allocated_bytes.all.current"] / (1024 ** 2), "MB")
5. What are possible problems with reducing the 384\times5\times5 representation to a 10\times5\times5 representation in one step?
Reducing the 384×5×5 representation to a 10×5×5 representation in one step in Network in Network (NiN) architecture can lead to several potential problems:
-
Loss of Information: Reducing the representation from 384 channels to only 10 channels in a single step can result in a significant loss of information. Each channel contains specific features and patterns learned by the network, and reducing them abruptly might lead to loss of discriminative power.
-
Underfitting: The reduced 10-channel representation might not have enough capacity to capture the complexity of the original input. This can result in the model underfitting the data, leading to poor generalization and performance.
-
Information Bottleneck: Such a drastic reduction in the number of channels creates an information bottleneck, limiting the network’s ability to transform the input effectively. It can hinder the network’s learning capability and limit its expressive power.
-
Reduced Expressiveness: Reducing the number of channels too quickly can limit the model’s ability to learn high-level features and hierarchical representations of the input data. Deep networks often rely on progressively learning more abstract features.
-
Spatial Features: A representation of 10×5×5 doesn’t capture spatial features well. Important spatial patterns and relationships present in the original representation might be lost, making the network less capable of recognizing objects.
-
Loss of Discriminative Power: With a smaller representation, the network might struggle to differentiate between different classes, leading to confusion and decreased accuracy.
To mitigate these problems, it’s common to use intermediate layers with smaller reductions in the number of channels, allowing the network to learn gradually more abstract and complex features. The NiN architecture typically uses multiple consecutive NiN blocks to avoid these issues by applying multiple nonlinear transformations with 1\times1 convolutions, gradually reducing the number of channels over several steps, and maintaining the network’s ability to learn meaningful representations.
6. Use the structural design decisions in VGG that led to VGG-11, VGG-16, and VGG-19 to design a family of NiN-like networks.
arch = ((96,11,4,0,2),(256,5,1,2,2),(384,3,1,1,2),(10,3,1,1,2))
nin = Nin(arch)
nin
Nin(
(net): Sequential(
(0): Sequential(
(0): LazyConv2d(0, 96, kernel_size=(11, 11), stride=(4, 4))
(1): ReLU()
(2): LazyConv2d(0, 96, kernel_size=(1, 1), stride=(1, 1))
(3): ReLU()
(4): LazyConv2d(0, 96, kernel_size=(1, 1), stride=(1, 1))
(5): ReLU()
)
(1): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(2): Sequential(
(0): LazyConv2d(0, 256, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(1): ReLU()
(2): LazyConv2d(0, 256, kernel_size=(1, 1), stride=(1, 1))
(3): ReLU()
(4): LazyConv2d(0, 256, kernel_size=(1, 1), stride=(1, 1))
(5): ReLU()
)
(3): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(4): Sequential(
(0): LazyConv2d(0, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU()
(2): LazyConv2d(0, 384, kernel_size=(1, 1), stride=(1, 1))
(3): ReLU()
(4): LazyConv2d(0, 384, kernel_size=(1, 1), stride=(1, 1))
(5): ReLU()
)
(5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(6): Dropout(p=0.5, inplace=False)
(7): Sequential(
(0): LazyConv2d(0, 10, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU()
(2): LazyConv2d(0, 10, kernel_size=(1, 1), stride=(1, 1))
(3): ReLU()
(4): LazyConv2d(0, 10, kernel_size=(1, 1), stride=(1, 1))
(5): ReLU()
)
(8): AdaptiveAvgPool2d(output_size=(1, 1))
(9): Flatten(start_dim=1, end_dim=-1)
)
)
arch15 = ((64,3,2,1),
(256,3,1,1),
(256,3,1,1),
(384,3,1,1),
(10,3,1,1))
nin15 = Nin(arch15)
nin15
Nin(
(net): Sequential(
(0): Sequential(
(0): LazyConv2d(0, 64, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
(1): ReLU()
(2): LazyConv2d(0, 64, kernel_size=(1, 1), stride=(1, 1))
(3): ReLU()
(4): LazyConv2d(0, 64, kernel_size=(1, 1), stride=(1, 1))
(5): ReLU()
)
(1): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(2): Sequential(
(0): LazyConv2d(0, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU()
(2): LazyConv2d(0, 256, kernel_size=(1, 1), stride=(1, 1))
(3): ReLU()
(4): LazyConv2d(0, 256, kernel_size=(1, 1), stride=(1, 1))
(5): ReLU()
)
(3): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(4): Sequential(
(0): LazyConv2d(0, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU()
(2): LazyConv2d(0, 256, kernel_size=(1, 1), stride=(1, 1))
(3): ReLU()
(4): LazyConv2d(0, 256, kernel_size=(1, 1), stride=(1, 1))
(5): ReLU()
)
(5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(6): Sequential(
(0): LazyConv2d(0, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU()
(2): LazyConv2d(0, 384, kernel_size=(1, 1), stride=(1, 1))
(3): ReLU()
(4): LazyConv2d(0, 384, kernel_size=(1, 1), stride=(1, 1))
(5): ReLU()
)
(7): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(8): Dropout(p=0.5, inplace=False)
(9): Sequential(
(0): LazyConv2d(0, 10, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU()
(2): LazyConv2d(0, 10, kernel_size=(1, 1), stride=(1, 1))
(3): ReLU()
(4): LazyConv2d(0, 10, kernel_size=(1, 1), stride=(1, 1))
(5): ReLU()
)
(10): AdaptiveAvgPool2d(output_size=(1, 1))
(11): Flatten(start_dim=1, end_dim=-1)
)
)